
Tüm Asal Sayılar Nelerdir?
Asal sayılar, sadece 1 ve kendisi tarafından tam bölünebilen pozitif tam sayılardır. Matematikte önemli bir yere sahip olmalarının yanı sıra, kriptografi ve sayılar teorisi gibi birçok alanda da kullanılır. Bu yazı, asal sayıların tanımını, özelliklerini ve tarihçesini ele almaktadır.
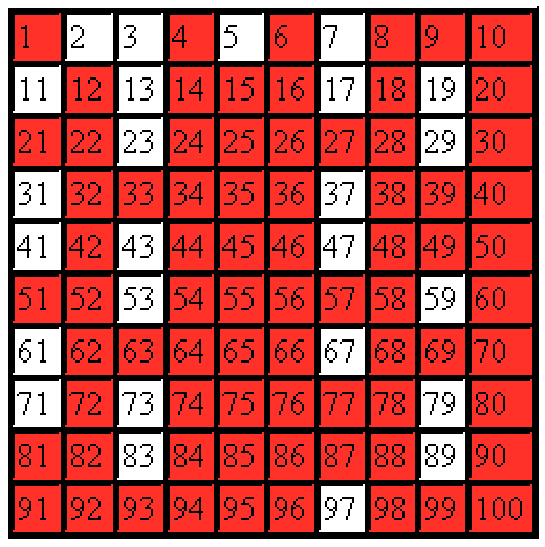
Asal sayılar, matematikte önemli bir konuma sahip olan pozitif tam sayılardır. Bir asal sayı, yalnızca 1 ve kendisi tarafından tam bölünebilen bir doğal sayıdır. Bu tanım, asal sayıların temel özelliklerini anlamak için kritik öneme sahiptir. Bu makalede, asal sayıların tanımından başlayarak, özelliklerine, tarihçesine ve kullanım alanlarına kadar kapsamlı bir inceleme yapacağız. Asal Sayıların Tanımı Asal sayılar, 1 ve kendisi dışında hiçbir pozitif tam sayıya bölünemeyen sayılardır. Örneğin;
Bu sayılar, asal sayılar olarak kabul edilir. 2, tek asal sayı olmasının yanı sıra, aynı zamanda tek çift asal sayıdır. Diğer tüm asal sayılar ise tektir. Asal Sayıların Özellikleri Asal sayıların çeşitli önemli özellikleri bulunmaktadır:
Asal Sayıların Tarihçesi Asal sayıların keşfi, antik çağlara kadar uzanmaktadır. Eski Yunan matematikçileri, özellikle Euclid, asal sayılar ve onların bölünebilirlik özellikleri üzerine önemli çalışmalar yapmışlardır. Euclid, asal sayıların sonsuz sayıda olduğunu kanıtlayan ilk matematikçi olarak bilinir. Bu eser, matematiğin temel taşlarından biri olarak kabul edilmektedir. Asal Sayıların Kullanım Alanları Asal sayılar, yalnızca teorik matematikte değil, aynı zamanda pratik uygulamalarda da önemli bir rol oynamaktadır. Öne çıkan birkaç kullanım alanı şunlardır:
Sonuç Asal sayılar, matematiğin temel yapı taşlarından biridir ve sayı teorisinin derinliklerine inmeyi sağlayan önemli bir konudur. Bu sayılar, tarih boyunca birçok matematiksel çalışmanın merkezinde yer almış ve günümüzde de çeşitli uygulama alanlarında kullanılmaya devam etmektedir. Asal sayıların sonsuzluğu ve benzersizliği, matematiksel keşiflerin kapılarını aralayan bir unsur olarak karşımıza çıkmaktadır. Matematiksel merak ve araştırma, bu asal sayılar hakkında daha fazla bilgi edinmemizi sağlayacak ve matematiğin derinliklerinde yeni keşiflere yol açacaktır. |






Rasyonel sayılar nedir
Rasyonel sayılar, iki tam sayının birbirine oranı şeklinde ifade edilebilen sayılardır. Yani bir sayıyı \( \frac{a}{b} \) biçiminde yazabiliyorsak, bu sayı rasyoneldir. Burada \( a \) ve \( b \) tam sayılardır ve \( b \) sıfırdan farklı olmalıdır. Örneğin, \( \frac{1}{2} \), \( -3 \) (çünkü \( \frac{-3}{1} \) şeklinde yazılabilir) veya \( 0.75 \) (çünkü \( \frac{3}{4} \)'e eşittir) rasyonel sayılardır.
Rasyonel sayılar kümesi genellikle \( \mathbb{Q} \) sembolüyle gösterilir ve şu özelliklere sahiptir:
Tanımı: \( \frac{a}{b} \) formundaki sayılar, burada \( a \) ve \( b \) tam sayı, \( b \neq 0 \).
Örnekler: \( \frac{2}{3} \), \( -5 \), \( 0 \), \( 1.25 \) (çünkü \( \frac{5}{4} \)).
Ondalık Gösterim: Rasyonel sayılar sonlu veya tekrarlayan ondalık sayılar olarak yazılabilir. Örneğin, \( \frac{1}{4} = 0.25 \) (sonlu), \( \frac{1}{3} = 0.333... \) (tekrarlayan).
İşlemler: Rasyonel sayılarla toplama, çıkarma, çarpma ve bölme (sıfıra bölme hariç) yapılabilir ve sonuç yine bir rasyonel sayıdır.
Kısacası, rasyonel sayılar günlük hayatta sıkça kullandığımız kesirler ve ondalık sayıları kapsar. Bu konuda başka bir sorun olursa, yardımcı olmaktan memnuniyet duyarım irem hanım.
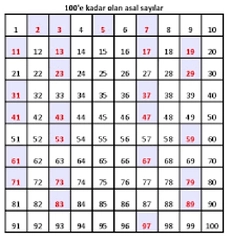
Asal sayılar hakkında yazılan bu metin oldukça bilgilendirici. Özellikle asal sayıların tanımı ve tarihçesi üzerinde durulması, bu konunun önemini vurguluyor. Asal sayıların yalnızca 1 ve kendisine bölünebildiği gerçeği, matematikteki birçok temel konseptin anlaşılmasına yardımcı oluyor. Ayrıca, 1 sayısının neden asal sayılmadığına dair yapılan açıklama da oldukça net. Eratosthenes'in kalburu ile asal sayıların bulunması yöntemi de pratik bir yaklaşım sunuyor. Acaba bu yöntemle asal sayıları bulmayı hiç denediniz mi? Özellikle genç matematik meraklıları için eğlenceli bir aktivite olabilir.
Yorumunuz İçin Teşekkürler Hacib
Asal sayılar hakkında yazılan metnin bilgilendirici olduğunu belirtmeniz çok güzel. Asal sayıların tanımı ve tarihçesi, matematiğin temel taşlarını anlamak için gerçekten önemlidir. Özellikle 1 sayısının asal sayı olarak kabul edilmemesi, bu konudaki karmaşayı gidermekte yardımcı oluyor.
Eratosthenes'in kalburu gibi yöntemlerin pratikte uygulanabilir olması, hem eğlenceli hem de öğretici bir deneyim sunuyor. Bu tür matematiksel aktiviteler, gençlerin matematiğe olan ilgisini artırmak için harika bir yol. Eğer bu yöntemi denemediyseniz, kesinlikle denemenizi öneririm; hem yeni şeyler öğrenir hem de zaman geçirirsiniz. Matematikle ilgili bu tür keşifler, meraklı zihinler için her zaman keyifli olmuştur.