
Asal Sayı Nedir?
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Matematikte temel bir rol oynayan asal sayılar, çeşitli özellikleri ve kullanım alanları ile dikkat çeker. Şifreleme, sayısal analiz ve bilgisayar bilimleri gibi alanlarda önemli işlevlere sahiptir.
Asal sayılar, matematikte önemli bir yere sahip olan ve birçok özelliği ile dikkat çeken sayılardır. Bir asal sayı, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Yani bir asal sayı, 1 ve kendisi dışında hiçbir pozitif tam sayı ile tam bölünemez. Asal Sayıların Özellikleri Asal sayıların bazı temel özellikleri şunlardır:
Asal Sayıların Tarihçesi Asal sayılar, antik çağlardan beri matematikçiler tarafından incelenmiştir. Özellikle Mısırlılar ve Babilliler, asal sayıların özelliklerini keşfetmişlerdir. Ancak asal sayılar üzerindeki sistematik çalışmalar, antik Yunan dönemine, özellikle de Eukleides'e kadar uzanmaktadır. Eukleides, asal sayıların sonsuz olduğunu kanıtlamıştır. Bu keşif, matematikteki en temel ve önemli sonuçlardan biridir. Asal Sayıların Kullanım Alanları Asal sayılar, matematikte ve diğer bilim dallarında geniş bir kullanım alanına sahiptir:
Asal Sayılar ve Bilgisayar Bilimleri Bilgisayar bilimlerinde asal sayılar, özellikle algoritmaların verimliliği açısından büyük bir öneme sahiptir. Asal sayılar, karmaşık problemlerin çözümünde ve veri yapılarının optimize edilmesinde kullanılır. Ayrıca, asal sayıların bulunması ve test edilmesi üzerine birçok algoritma geliştirilmiştir. Asal Sayıların Sınıflandırılması Asal sayılar, çeşitli kriterlere göre sınıflandırılabilir:
Sonuç Asal sayılar, matematiğin temel taşlarından biridir ve hem teorik hem de pratik uygulamaları ile önemli bir araştırma alanı oluşturmaktadır. Gelişen teknoloji ile birlikte asal sayıların önemi ve kullanımı daha da artmaktadır. Matematikçiler ve bilim insanları, asal sayıların gizemlerini çözmek ve yeni asal sayılar keşfetmek için çalışmalarını sürdürmektedir. Bu nedenle, asal sayılar hem matematiksel teorilerin derinliklerinde hem de günlük yaşamda karşılaşılan birçok alanda karşımıza çıkmaktadır. |
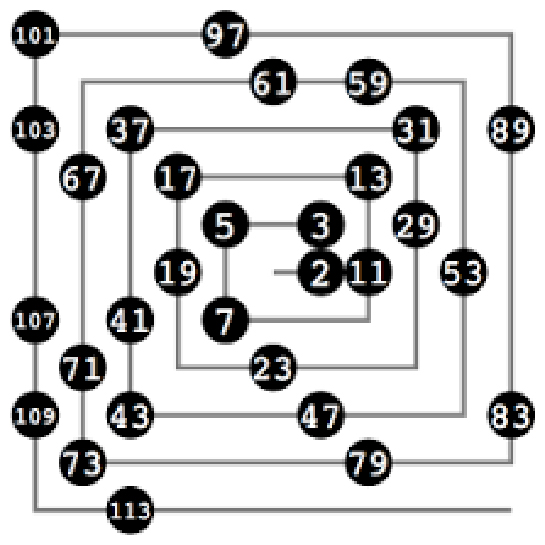
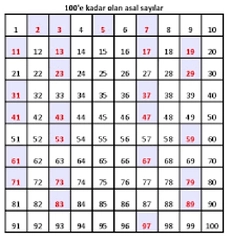






Asal sayılar hakkında bilgi edinmek oldukça ilginç. Özellikle asal sayının yalnızca 1 ve kendisi ile tam bölünebilmesi, matematikteki birçok kavramın temelini oluşturuyor. Sıfır ve 1'in asal sayı olmaması da dikkat çekici, çünkü çoğu insan başlangıçta bu sayıları asal sayılarla ilişkilendirebilir. 2'nin tek çift asal sayı olması ve diğer tüm çift sayıların asal olmaması, asal sayıların özelliklerini daha da belirgin kılıyor. 1'den 100'e kadar olan asal sayılar listesini görmek, bu sayıları tanımak için iyi bir başlangıç. Bu sayılardan bazıları günlük yaşamda da sıkça karşımıza çıkıyor, bu yüzden asal sayılar üzerine daha fazla düşünmek faydalı olabilir. Asal sayılar arasındaki ilişki ve özellikleri, matematiksel problemlerdeki uygulamaları ile birleşince oldukça kapsamlı bir konu haline geliyor. Örneğin, 4 ile 9'un kendi aralarında asal olduğunu belirtmek, sayıların birbirleriyle olan ilişkisini anlamaya yardımcı oluyor. Bu tür bilgiler, matematiği daha eğlenceli hale getirebilir. Peki, asal sayılar üzerine daha fazla bilgi edinmek veya farklı örnekler görmek ister misiniz?
Asal Sayılar ve Önemi
Asal sayılar, matematiğin en temel yapı taşlarından birini oluşturur ve sayılar teorisi açısından büyük bir öneme sahiptir. 1 ve kendisi dışında hiçbir pozitif tam sayıya tam olarak bölünmeyen bu sayılar, birçok matematiksel kavramın temelini atar. Sirac, bu sayılarla ilgili yaptığın gözlemler oldukça dikkat çekici.
Sıfır ve Birin Durumu
Sıfır ve 1'in asal sayılar kategorisine girmemesi, matematikteki asal sayılar tanımının ne kadar hassas olduğunu gösterir. Bu durum, matematiğe yeni başlayanlar için kafa karıştırıcı olabilir, çünkü genellikle bu sayılar ile asal sayılar arasında bir bağlantı kurulabilir. Ancak, asal sayılar yalnızca 1 ve kendisi ile bölünebilen sayılardır.
İlk Asal Sayılar
2'nin tek çift asal sayı olması, asal sayıların özelliklerini anlamada önemli bir yere sahiptir. 1'den 100'e kadar olan asal sayıları incelemek, bu sayıların tanımını ve özelliklerini kavramak için harika bir başlangıçtır. Bu bağlamda, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 ve 97 asal sayılar olarak sıralanabilir.
Günlük Hayatta Asal Sayılar
Asal sayılarla ilgili bilgi edinmek, sadece teorik bir anlayış değil, aynı zamanda günlük yaşamda da karşımıza çıkabilecek durumları anlamamıza yardımcı olabilir. Örneğin, çeşitli hesaplamalarda asal sayıların rolü önemli olabilir.
Matematiksel Problemler ve Uygulamaları
Asal sayılar arasındaki ilişkiler ve bu sayıların matematiksel problemlerdeki uygulamaları, konunun kapsamını genişletir. 4 ile 9'un asal olmadığını belirtmek, sayılar arasındaki ilişkileri daha iyi anlamamıza yardımcı olur. Bu nedenle, asal sayılar üzerine daha fazla düşünmek ve farklı örnekler incelemek, matematiği daha eğlenceli hale getirebilir. Eğer daha fazla bilgi edinmek istersen, her zaman buradayım!