
En Büyük Asal Sayı Kaçtır?
Asal sayılar, yalnızca 1 ve kendisi tarafından tam bölünebilen pozitif tam sayılardır. Bu yazıda asal sayıların tanımı, özellikleri, tarihçesi ve en büyük asal sayının belirlenmesi gibi konular ele alınacaktır. Ayrıca, asal sayıların modern bilimdeki önemine de değinilecektir.
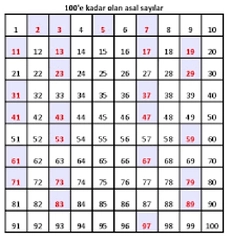
Asal sayılar, sadece 1 ve kendisi olmak üzere tam bölenleri olan pozitif tam sayılardır. Matematikte asal sayılar, sayılar teorisi açısından önemli bir yer tutar ve birçok alanda uygulama alanı bulur. Bu makalede, en büyük asal sayının ne olduğu, asal sayıların özellikleri ve en büyük asal sayının bulunma yöntemleri ele alınacaktır. Asal Sayıların Tanımı ve Özellikleri Asal sayılar, 1 ve kendisi dışında hiçbir pozitif tam sayıya bölünmeyen sayılardır. Örneğin, 2, 3, 5, 7, 11, 13 gibi sayılar asal sayılardır. Asal sayıların bazı önemli özellikleri şunlardır:
Asal Sayıların Tarihçesi Asal sayılar, antik dönemlerden beri matematikçilerin ilgisini çekmiştir. Öne çıkan bazı tarihsel noktalar şunlardır:
En Büyük Asal Sayının Belirlenmesi En büyük asal sayıyı bulma süreci, oldukça karmaşık ve zorlu bir matematiksel problemdir. Günümüzde bilinen en büyük asal sayılar genellikle bilgisayar yardımı ile keşfedilmektedir. En büyük bilinen asal sayı, 2022 itibarıyla 2^82,589,933 - 1 olarak tanımlanan Mersenne asal sayısıdır ve yaklaşık 24,862,048 basamaktan oluşmaktadır. Bu sayı, GIMPS (Great Internet Mersenne Prime Search) adlı bir projeyle bulunmuştur. Mersenne Asal Sayıları Mersenne asal sayıları, formülü 2^p - 1 şeklinde tanımlanan asal sayılardır. Burada p, asal bir sayıdır. Mersenne asal sayılarının bazı özellikleri şunlardır:
Asal Sayılar ve Günümüz Bilimindeki Önemi Asal sayılar, günümüzde birçok alanda kullanılmaktadır. Özellikle şifreleme ve güvenlik alanında asal sayıların kullanımı oldukça yaygındır. Örnekler:
Sonuç Asal sayılar, matematiksel yapının temel taşlarıdır ve en büyük asal sayının bulunması matematiksel araştırmaların önemli bir konusu olmaya devam etmektedir. Bilgisayar teknolojilerinin ilerlemesi ile birlikte, daha büyük asal sayıların keşfi mümkün hale gelmiştir. Asal sayıların teorisi ve uygulamaları, matematik ve ilgili bilim dallarında önemli bir yer tutmaktadır. Ekstra Bilgiler Asal sayılarla ilgili yapılan araştırmalar, matematiksel teorilerin yanı sıra hesaplama yöntemlerinin de gelişmesine katkı sağlamaktadır. Asal sayıların bulunması ve bu sayılar üzerindeki çalışmalar, matematiksel düşüncenin derinleşmesine ve yeni yöntemlerin geliştirilmesine zemin hazırlamaktadır. |







Dr. Curtis Cooper'ın keşfettiği bu devasa asal sayının kağıda yazılmasını hayal bile edemiyorum, gerçekten 109 kilometre mi sürecek? Bu kadar uzun bir sayının dijital güvenlik sistemlerinde kullanılması ne gibi avantajlar sağlıyor olabilir?
Seyhan, Dr. Curtis Cooper'ın keşfettiği bu devasa asal sayının kağıda yazılması gerçekten inanılmaz bir düşünce. Evet, bu sayının uzunluğu 109 kilometreyi bulabilir ve bu gerçekten akıl almaz bir büyüklük. Dijital güvenlik sistemlerinde bu tür büyük asal sayıların kullanılması, özellikle şifreleme algoritmalarında büyük avantajlar sağlar. Çünkü büyük asal sayılar, faktorizasyon işlemini zorlaştırır ve bu da şifrelerin kırılmasını oldukça güçleştirir. Bu sayede, verilerin daha güvenli bir şekilde korunması mümkün olur.