
1'den 100'e Kadar Asal Sayılar Nelerdir?
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan sayılardır. Matematikteki temel kavramlardan biri olan asal sayılar, birçok teorinin ve uygulamanın temelini oluşturur. Bu içerikte, 1'den 100'e kadar olan asal sayılar, özellikleri ve tarihçesi ele alınmaktadır.
Asal sayılar, yalnızca 1 ve kendisi olmak üzere tam bölenleri olan, 1'den büyük pozitif tam sayılardır. Matematikte asal sayılar, sayı teorisinin en temel ve önemli konularından biridir. Asal sayılar, birçok matematiksel kavramın ve teorinin temelini oluşturur. Bu makalede, 1'den 100'e kadar olan asal sayıları inceleyeceğiz, bu asal sayıların özelliklerini tartışacağız ve asal sayıların tarihçesi ile uygulama alanlarına değineceğiz. Asal Sayıların Tanımı Asal sayılar, yalnızca iki pozitif böleni olan sayılardır:
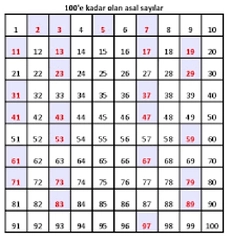
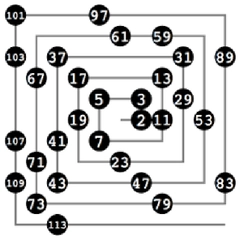
Örneğin, 2, 3, 5, 7 gibi sayılar asal sayılardır. Ancak 4, 6, 8, 9 gibi sayılar asal değildir çünkü bu sayılar, 1 ve kendisi dışında başka bölenlere sahiptir. 1'den 100'e Kadar Olan Asal Sayılar 1'den 100'e kadar olan asal sayılar şunlardır:
Bu liste, 1'den 100'e kadar olan asal sayıların tam bir dökümünü sunmaktadır. Görüldüğü gibi, 2 en küçük asal sayıdır ve ayrıca tek çift asal sayıdır. Tüm diğer asal sayılar ise tektir. Asal Sayıların Özellikleri Asal sayıların bazı önemli özellikleri şunlardır:
Asal Sayıların Tarihçesi Asal sayılar, eski çağlardan beri matematikçilerin ilgi alanında olmuştur. Eski Yunan matematikçisi Eratosthenes, asal sayıları bulmak için bir yöntem geliştirmiştir. Bu yöntem, "Süzgeç" (Sieve) olarak bilinir ve belirli bir aralıktaki asal sayıları bulmak için etkili bir yöntemdir. Bu yöntem, sıralı bir liste oluşturarak, asal sayıları belirleyerek çalışır. Asal Sayıların Uygulama Alanları Asal sayılar, matematikte birçok alanda uygulama bulur. Öne çıkan bazı alanlar şunlardır:
Sonuç Asal sayılar, matematik biliminin temel yapı taşlarından biri olup, 1'den 100'e kadar olan asal sayılar, matematiksel araştırmalarda ve uygulamalarda önemli bir yer tutmaktadır. Bu sayılar, yalnızca sayı teorisi ile sınırlı kalmayıp, kriptografi ve bilgisayar bilimleri gibi alanlarda da geniş bir uygulama yelpazesine sahiptir. Asal sayıların özelliklerini anlamak, matematiksel düşüncenin gelişmesine katkıda bulunur. |






Asal sayılarla ilgili yazdıklarınızı okuduktan sonra gerçekten merak ediyorum, 2 sayısının asal sayılar arasında neden bu kadar özel bir yere sahip olduğunu düşünüyorsunuz? Aslında, 2 sayısı dışındaki tüm çift sayılar, 2'ye bölünebildikleri için asal olamıyorlar. Bu durum, 2'yi tek çift asal sayı haline getiriyor. Diğer asal sayılar ise tek oldukları için kendilerine özgü bir yapıya sahip. Bu durum, asal sayıların genel özellikleriyle ilgili ilginç bir istisna yaratıyor. Asal sayılar arasında böyle bir ayrımın olması, matematikteki bazı kuralların ne kadar esnek olabileceğini gösteriyor. Sizce, asal sayılar arasında bu tür farklılıklar daha fazla keşfedilmeyi bekliyor mu?
Merhaba Meziyet,
2 sayısının asal sayılar arasındaki özel yerini vurguladığınız için teşekkür ederim. Gerçekten de 2, diğer asal sayılardan farklı olarak tek bir çift asal sayıdır. Bu durum, matematikteki asal sayılarla ilgili olan birçok ilginç özelliğin temelini oluşturuyor. Asal sayılar, sayılar teorisi açısından çok önemli bir yere sahip ve 2'nin çift olmasının yanı sıra, tek sayılar arasındaki yerinin de matematiksel araştırmalara ilham verdiği görülüyor.
Asal Sayıların Özellikleri
Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan sayılardır. Bu tanım, asal sayıların yapısının yanı sıra, sayı teorisi içerisindeki yerini de belirler. 2'nin çift olması, onu diğer asal sayılardan ayırırken, matematiksel kuralları sorgulama ve daha derinlemesine keşif yapma fırsatı sunuyor. Asal sayılar arasındaki bu farklılıklar, matematikteki bazı kuralların neden esnek olabileceğini de gösteriyor.
Keşfedilmeyi Bekleyen Farklılıklar
Asal sayılar hakkında daha fazla keşif yapılması gerektiği kesinlikle doğru. Matematikte her zaman yeni teoriler ve anlayışlar geliştirilmekte, asal sayılarla ilgili birçok problem hala tam olarak çözülememiş durumdadır. Özellikle asal sayıların dağılımı ve özellikleri üzerine yapılan çalışmalar, matematiksel düşünceyi zenginleştiriyor ve yeni keşiflere kapı açıyor. Bu anlamda, 2 sayısının asal sayılar arasındaki yeri, matematiksel düşünceyi derinleştirmenin bir yolu olarak görülebilir.
Sonuç olarak, asal sayılar arasındaki bu tür farklar, matematikteki keşiflerin ve yeniliklerin devam etmesine olanak tanıyor. 2'nin özel durumu, daha geniş matematiksel yapıların ve kuralların keşfedilmesi için bir başlangıç noktası olabilir.
Saygılarımla,
Bu yazıda belirtildiği gibi, asal sayıların özel durumları var mıdır? Mesela, 2 sayısı neden tek çift asal sayı olarak kabul edilir ve diğer çift sayılar neden asal değildir?
Gökmen Bey, 2 sayısının tek çift asal sayı olarak kabul edilmesinin sebebi, asal sayıların tanımında yatmaktadır. Asal sayılar, sadece 1 ve kendisiyle tam bölünebilen pozitif tam sayılardır. 2 sayısı bu tanıma uyan tek çift sayıdır. Diğer çift sayılar ise en azından 1, kendisi ve 2'ye bölünebildikleri için asal sayı olamazlar. Bu yüzden, 2 asal sayıların arasında özel bir yer tutar.