Aralarındaki Asal Sayılar Nasıl Bulunur?Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan sayılardır. Matematiksel olarak asal sayılar, sayı teorisi içinde önemli bir yere sahiptir ve birçok alanda uygulama alanı bulmaktadır. Bu makalede, asal sayıları bulmanın yöntemleri ve aralarındaki asal sayıların belirlenmesi üzerine detaylı bir inceleme yapılacaktır. Asal Sayıların Tanımı ve ÖzellikleriAsal sayılar, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 gibi sayıların oluşturduğu bir kümedir. Bu sayıların en temel özelliği, yalnızca iki pozitif böleni olmasıdır. 1 ve kendisi dışında hiçbir pozitif tam böleni yoktur. Ayrıca, 2 en küçük ve tek çift asal sayıdır; diğer asal sayılar ise tektir. Asal Sayıları Bulma YöntemleriAsal sayıları bulmak için çeşitli yöntemler geliştirilmiştir. Bu yöntemler arasında en yaygın olanları şunlardır:
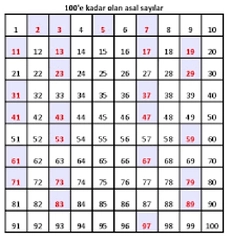
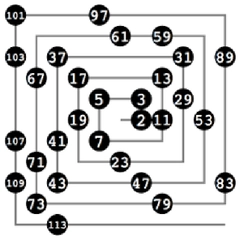
Sieve of Eratosthenes (Eratosthenes Eleği)Eratosthenes Eleği, n'e kadar olan asal sayıları bulmak için etkili bir yöntemdir. Bu yöntemde, 2'den n'e kadar olan tüm sayılar bir listeye alınır. Ardından, 2'den başlayarak her asal sayı için, bu asal sayının katları listeden çıkarılır. Bu işlem, listeyi tamamlayana kadar devam eder. Sonuç olarak, geriye kalan sayılar asal sayılardır. Trial Division (Deneme Bölme)Deneme bölme yöntemi, bir sayının asal olup olmadığını belirlemek için kullanılan basit bir tekniktir. Bu yöntemde, n sayısını 2'den √n'ye kadar olan her asal sayı ile böleriz. Eğer n, bu asal sayılardan hiçbiri tarafından tam bölünmüyorsa, o zaman n asal bir sayıdır. Miller-Rabin Asal TestiMiller-Rabin testi, büyük sayılar için hızlı bir asal belirleme yöntemidir. Bu yöntem, n sayısının asal olup olmadığını belirlemek için rastgele seçilen tabanlar kullanır. Eğer n, belirli tabanlara göre asal ise, n'nin asal olma olasılığı yüksektir. Ancak bu test, kesin sonuç değil, olasılık sunar. AKS Asal TestiAKS asal testi, belirli bir sayının asal olup olmadığını belirlemenin polinomik bir yoludur. Bu test, n sayısının asal olup olmadığını tespit etmek için polinomların özelliklerini kullanır. AKS testi, kesin bir sonuç verir ve belirli bir karmaşıklıkta çalışır. SonuçAsal sayılar, matematiğin temel yapı taşlarından biridir ve aralarındaki asal sayıların bulunması, birçok farklı yöntemle gerçekleştirilebilir. Bu yöntemlerin her birinin kendine has avantajları ve dezavantajları vardır. Asal sayıları bulma teknikleri, hem teorik hem de pratik uygulamalarda önemli bir yere sahiptir. Matematiksel araştırmalar ve uygulamalar, asal sayıların doğasına dair daha derin anlayışlar geliştirmek için devam etmektedir. Ekstra Bilgiler |
Asal sayıları bulmanın bu kadar farklı ve etkili yöntemleri olduğunu öğrenince, gerçekten hayret ettim. Özellikle Eratosthenes Eleği'nin nasıl çalıştığını anlamak, bu konudaki en temel bilgileri edinmemi sağladı. Ben de asal sayıların bu kadar önemli bir yere sahip olduğunu düşünüyordum ama kriptografi gibi modern uygulamalarında da ne denli kritik rol oynadıklarını öğrenmek beni daha da etkiledi. Peki, bu yöntemlerin avantajları ve dezavantajları neler? Özellikle büyük asal sayıları bulmak için hangi yöntemi tercih edersiniz?
Cevap yazMebruk,
Asal Sayıların Önemi
Asal sayılar, matematikte ve çeşitli uygulamalarda önemli bir yere sahiptir. Özellikle kriptografi alanında, asal sayıların kullanımı güvenli iletişim sağlamada kritik bir rol oynar. Bu nedenle, asal sayıları bulma yöntemlerini anlamak oldukça faydalı.
Eratosthenes Eleği
Eratosthenes Eleği, asal sayıları bulmak için oldukça etkili bir yöntemdir. Bu yöntem, belirli bir aralıktaki tüm sayıları elekten geçirerek asal sayıları belirler. Avantajı, basitliği ve etkinliğidir. Ancak, büyük sayılar için bellek kullanımı artabilir ve işlem süresi uzayabilir.
Diğer Yöntemler
Büyük asal sayılar bulmak için Miller-Rabin testi gibi probabilistik yöntemler veya AKS asal testi gibi deterministik yöntemler tercih edilebilir. Probabilistik yöntemler genellikle daha hızlıdır, ancak kesin sonuç vermez. Deterministik yöntemler ise daha güvenilir olsa da, işlem süresi daha uzundur.
Sonuç
Büyük asal sayılar bulmak için hangi yöntemi seçeceğiniz, ihtiyaçlarınıza ve mevcut kaynaklarınıza bağlıdır. Eğer hızlı bir sonuç arıyorsanız probabilistik yöntemler tercih edilebilir. Ancak, kesinlikle doğruluk istiyorsanız deterministik yöntemleri değerlendirmek daha uygun olacaktır.