
8. Sınıf Asal Sayılar Konu Anlatımı
Asal sayılar, matematikte temel bir yapı taşını oluşturur. Bu makalede, 8. sınıf düzeyinde asal sayıların tanımı, özellikleri, kullanım alanları ve bulma yöntemleri hakkında ayrıntılı bilgiler sunulmaktadır. Öğrencilerin matematiksel düşünme becerilerini geliştirmelerine yardımcı olur.
8. Sınıf Asal Sayılar Konu AnlatımıAsal sayılar, matematikte önemli bir yere sahip olan ve birçok kavramın temelini oluşturan özel sayılardır. Bu makalede, 8. sınıf düzeyinde asal sayılar konusunu ayrıntılı bir biçimde ele alacağız. Asal sayılar, çok sayıda matematiksel problemde ve teoride kritik bir rol oynamaktadır. Asal Sayı Nedir? Asal sayılar, yalnızca 1 ve kendisi olmak üzere tam iki pozitif böleni olan sayılardır. Yani, bir asal sayı, 1 ve o sayının kendisi dışında hiçbir pozitif tam sayıya tam bölünemez. Örnek vermek gerekirse:
Yukarıda listelenen sayılar asal sayılardır. Buradan hareketle, 1 sayısının asal sayı olmadığını belirtmek gerekir; çünkü 1'in yalnızca bir pozitif böleni vardır. Asal Sayıların Özellikleri Asal sayılar, çeşitli özelliklere sahiptir. Bu özelliklerden bazıları şunlardır:
Asal Sayıların Kullanım Alanları Asal sayılar, birçok alanda kullanılmaktadır. Bu kullanım alanlarından bazıları şunlardır:
Asal Sayıları Bulma Yöntemleri Asal sayıları bulmak için farklı yöntemler ve algoritmalar geliştirilmiştir. Bu yöntemlerden bazıları şunlardır:
Sonuç Asal sayılar, matematiksel düşüncenin ve teorinin temel unsurlarından biridir. 8. sınıf düzeyinde asal sayılar konusunu anlamak, öğrencilere matematiksel mantık ve problem çözme becerileri kazandırır. Asal sayıların özellikleri ve kullanım alanları, matematik derslerinde önemli bir yere sahip olup, temel matematik bilgilerini pekiştirmeye yardımcı olur. Ekstra Bilgiler |
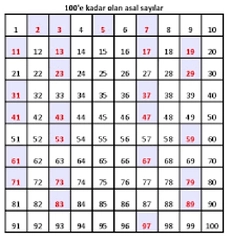

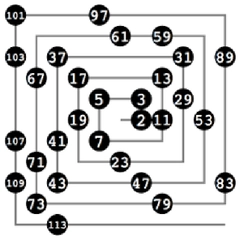





Asal sayılar hakkında yazılan bu makale gerçekten aydınlatıcı. Özellikle asal sayının tanımından başlayarak, özellikleri ve kullanım alanlarına kadar geniş bir perspektif sunmuş. Asal sayılarla ilgili en ilginç noktalardan biri, 2'nin tek asal sayı olması. Bu ayrıntıyı öğrenmek, asal sayılar konusundaki temel bilgilerimi pekiştirdi. Ayrıca, asal sayıların sonsuz sayıda olduğunu duymak, matematiğin ne kadar derin bir evren sunduğunu bir kez daha hatırlatıyor. Kriptografi gibi gerçek dünyada önemli uygulamalara sahip olması ise asal sayıların ne kadar kritik bir rol oynadığını gösteriyor. Erathosthenes Eleği gibi yöntemler ise asal sayıları bulmanın ne kadar sistematik bir şekilde yapılabileceğini gözler önüne seriyor. 8. sınıf düzeyinde bu konuyu öğrenmek, matematiksel düşünme becerilerimi geliştirmek için harika bir fırsat. Sizce asal sayılar üzerine daha fazla pratik yapmak, bu bilgilerin kalıcılığı açısından ne kadar önemlidir?
Yorumun İçeriği
Perkin, yazdığınız makalenin asal sayılar hakkındaki derinlemesine bilgi sunduğu için gerçekten memnun oldum. Asal sayıların tanımı, özellikleri ve kullanımları üzerine yaptığınız vurgular, bu konunun ne kadar önemli olduğunu gözler önüne seriyor. Özellikle 2'nin tek asal sayı olduğu bilgisi, pek çok kişi için dikkat çekici bir detay.
Pratik Yapmanın Önemi
Asal sayılar üzerine daha fazla pratik yapmanın, bu bilgilerin kalıcılığı açısından büyük bir önemi var. Matematiksel kavramları uygulamak, öğrenilen bilgilerin pekişmesini sağlarken, aynı zamanda problem çözme becerilerini de geliştirir. Yöntemler üzerinde çalışmak, Erathosthenes Eleği gibi sistematik yaklaşımları anlamanızı derinleştirir ve konuyu daha iyi kavramanızı sağlar.
Öneriler
Asal sayılarla ilgili daha fazla pratik yapmak için çeşitli matematiksel oyunlar veya bulmacalar çözmek, bu bilgileri hayatınıza entegre etmenin eğlenceli yollarından biridir. Ayrıca, asal sayılarla ilgili daha karmaşık problemlerle karşılaşmak, matematiksel düşünme becerilerinizi daha da geliştirebilir. Bu nedenle, konuyu daha derinlemesine öğrenmek için sürekli pratik yapmak oldukça faydalı olacaktır.