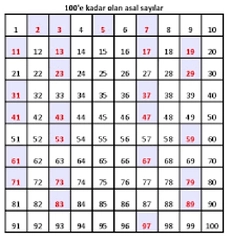
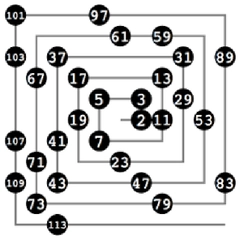
Asal sayılar, matematikte önemli bir yer tutan ve temel aritmetik yapı taşları olarak kabul edilen sayılardır. Bir asal sayı, yalnızca 1 ve kendisi olmak üzere tam bölenleri bulunan pozitif bir tam sayıdır. Bu makalede, 1'den 90'a kadar olan asal sayılar detaylı bir şekilde incelenecektir. Asal sayıların özellikleri, tarihçesi ve uygulamaları hakkında da bilgi verilecektir.Asal Sayıların TanımıAsal sayılar, doğal sayılar arasında yalnızca iki pozitif böleni olan sayılardır: 1 ve kendisi. Örneğin, 2, 3, 5, 7 gibi sayılar asal sayılardır. Ancak 4, 6, 8 gibi sayılar asal değildir çünkü bu sayılar 1 ve kendisi dışında başka bölenlere de sahiptir. 1'den 90'a kadar olan asal sayılar şunlardır:
Asal Sayıların ÖzellikleriAsal sayıların birkaç önemli özelliği vardır:
TarihçeAsal sayılar, antik Yunan dönemine kadar uzanan bir geçmişe sahiptir. Matematikçiler, asal sayıların özel özelliklerini incelemek için çeşitli teoriler geliştirmiştir. Örneğin, Euclid, asal sayıların sonsuzluğunu kanıtlayan ünlü bir teorem sunmuştur. Ayrıca, asal sayılar, kriptografi ve bilgisayar bilimlerinde de büyük öneme sahiptir. UygulamalarAsal sayılar, özellikle kriptografi alanında güvenlik protokollerinin temelini oluşturur. Asal sayıların büyük olması, şifreleme algoritmalarının güvenliğini artırır. Bunun yanı sıra, asal sayılar, algoritmaların verimliliğini artırmak için çeşitli matematiksel hesaplamalarda da kullanılır. SonuçAsal sayılar, matematiğin temel unsurlarından biri olup, birçok alanda uygulanabilirliği ve önemi ile dikkat çekmektedir. 1'den 90'a kadar olan asal sayılar, bu önemli kavramın ilk örneklerini oluşturur. Asal sayıların analizi, hem teorik hem de pratik açıdan matematiğin derinliklerine ulaşmamıza yardımcı olur. Ekstra BilgilerAsal sayılar üzerine yapılan araştırmalar, matematiksel teorilerin gelişimi açısından kritik bir rol oynamaktadır. Ayrıca, asal sayılar arasındaki ilişkilerin incelenmesi, yeni teorilerin ve yöntemlerin keşfine kapı aralamaktadır. Bilgisayar bilimlerinde, asal sayıların belirlenmesi ve sıralanması için kullanılan algoritmalar, büyük veri analizi ve işlemci performansı açısından önemli bir yere sahiptir. |
Asal sayılar hakkında yapılan bu inceleme gerçekten ilgi çekici. Özellikle asal sayıların matematikteki yeri ve önemi üzerine yapılan vurgular dikkatimi çekti. 1'den 90'a kadar olan asal sayıların listesi, bu sayıların nasıl bir yapıya sahip olduğunu anlamamı sağladı. Ayrıca, asal sayıların kriptografi gibi pratik uygulamalardaki rolü de oldukça etkileyici. Bu konuda daha fazla bilgi sahibi olmak, matematiğin derinliklerine dair merakımı artırıyor. Asal sayıların sonsuz sayıda olduğunu bilmek, matematiksel düşünme becerimizi nasıl geliştiriyor sizce?
Cevap yazAsal Sayılar ve Matematikteki Önemi
Müstebir, asal sayılar matematiğin temel taşlarından birini oluşturur ve bu sayıların özellikleri, birçok matematiksel teorinin temelini atar. Asal sayılar, 1 ve kendisi dışında hiçbir pozitif böleni olmayan sayılar olarak tanımlanır ve bu özellikleri onları özel kılar. Matematikteki yerleri, sayı teorisi gibi alanlarda derinlemesine incelenmektedir.
Asal Sayıların Yapısı
1'den 90'a kadar olan asal sayıların listesi, bu sayıların belirli bir düzen ve yapıya sahip olduğunu gösterir. Asal sayıların dağılımı, matematiksel araştırmalarda önemli bir rol oynar ve bu sayıların özellikleri üzerine yapılan çalışmalar, matematiğin daha derin kavramlarını anlamamıza yardımcı olur.
Pratik Uygulamalar
Kriptografi gibi alanlarda asal sayıların kullanımı, onların matematiksel öneminin yanı sıra günlük yaşamda ne kadar kritik bir rol oynadığını da gözler önüne seriyor. Güvenli iletişim ve veri koruma gibi konularda asal sayılara dayanan algoritmalar kullanmak, bu sayıların pratikteki etkileyici yönünü ortaya koyuyor.
Matematiksel Düşünme Becerileri
Asal sayıların sonsuz sayıda olduğunu bilmek, matematiksel düşünme becerilerimizi geliştirmeye yardımcı olur. Bu bilgi, matematiksel mantık ve soyut düşünme yeteneğimizi artırarak, problem çözme becerilerimizi de güçlendirir. Ayrıca, sonsuzluk fikri, matematiksel kavramların derinliğini ve karmaşıklığını anlamamıza katkı sağlar.
Sonuç olarak, asal sayılar üzerindeki bu tür incelemeler, matematiğe olan merakımızı körükler ve bu alandaki bilgi birikimimizi artırır.