Asal sayılar, yalnızca 1 ve kendisi olmak üzere tam bölenleri olan pozitif tam sayılardır. Matematikte önemli bir yer tutan asal sayılar, sayılar teorisi alanında temel bir yapı taşıdır. Bu makalede, 1'den 80'e kadar olan asal sayılar listelenecek ve asal sayıların özellikleri hakkında genel bilgiler verilecektir. Ayrıca, asal sayıların matematiksel ve pratik uygulamaları da ele alınacaktır. Asal Sayıların Tanımı ve ÖzellikleriAsal sayılar, iki pozitif böleni olan sayılardır. Bu bölenler 1 ve kendisidir. Asal sayıların bazı temel özellikleri şunlardır:
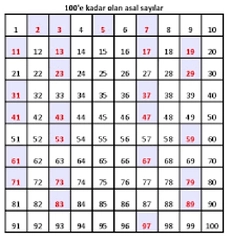
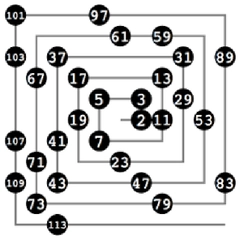
1'den 80'e Kadar Olan Asal Sayılar1'den 80'e kadar olan asal sayılar şunlardır:
Asal Sayıların Matematikteki ÖnemiAsal sayılar, matematiksel kavramların birçoğunun temelini oluşturmaktadır. Aşağıda asal sayıların matematikteki bazı önemli rolleri sıralanmıştır:
Asal Sayıların UygulamalarıAsal sayıların günlük yaşamda ve çeşitli bilimsel alanlarda birçok uygulaması bulunmaktadır. Bu uygulamalardan bazıları şunlardır:
SonuçAsal sayılar, matematikte ve birçok bilim dalında önemli bir yere sahiptir. 1'den 80'e kadar olan asal sayılar, bu sayıların temel özelliklerini ve uygulamalarını anlamak açısından büyük bir öneme sahiptir. Asal sayıların keşfi ve incelenmesi, matematiksel düşüncenin gelişmesine katkı sağlamaktadır. Gelecekteki çalışmalar, asal sayıların daha derin özelliklerini ve ilişkilerini ortaya çıkarma potansiyeline sahiptir. Bu makalede, asal sayılar hakkında temel bilgiler verilmiş olup, 1'den 80'e kadar olan asal sayıların listesi sunulmuştur. Asal sayıların matematiksel ve pratik uygulamaları, bu sayılara olan ilgiyi artırmakta ve araştırmalara yön vermektedir. |
Asal sayılar hakkında yazılan bu makale, matematiğin temel yapı taşlarından biri olan asal sayıları oldukça iyi özetlemiş. Asal sayıların tanımından başlayarak, özellikleri ve 1'den 80'e kadar olan asal sayıların listesi verilmesi çok faydalı. Özellikle asal sayıların şifreleme algoritmaları gibi pratik uygulamalardaki yerini vurgulamak, matematiğin günlük yaşamda ne kadar önemli bir rol oynadığını gösteriyor. Asal sayıların sonsuz sayıda olduğunun belirtilmesi ve bu konuda yapılan araştırmaların devam etmesi, bu alandaki merakımı artırıyor. Sizce de asal sayıların bu denli derin bir yapıya sahip olması, matematiksel düşünceyi geliştirmek için neden bu kadar önemli?
Cevap yazAsal Sayıların Derin Yapısı
Şölen, asal sayıların matematikteki yeri gerçekten de çok önemlidir. Asal sayılar, sayı teorisinin temel taşlarından biri olarak kabul edilir ve birçok matematiksel kavramın anlaşılmasına yardımcı olur. Bu sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır ve bu basit tanımın ötesinde, birçok ilginç özellik barındırırlar.
Matematiksel Düşünceyi Geliştirme
Asal sayıların derin yapısı, matematiksel düşünceyi geliştirmek için son derece önemlidir. Öncelikle, asal sayılar arasında bağlantılar kurmak, örüntüleri keşfetmek ve bu sayılarla ilgili problemleri çözmek, analitik düşünme becerilerini artırır. Ayrıca, asal sayıların şifreleme algoritmalarındaki uygulamaları, matematiğin pratik alanlarda nasıl kullanıldığını göstererek, matematiksel kavramların gerçek hayattaki önemini vurgular.
Sonuç ve Araştırmalar
Son olarak, asal sayıların sonsuz sayıda olduğunu ve bu alanda yapılan araştırmaların devam ettiğini bilmek, matematiksel merakı artıran bir unsurdur. Bu durum, matematiğin dinamik ve sürekli gelişen bir alan olduğunu gösterirken, aynı zamanda asal sayıların keşfedilmemiş sırlarının peşinde koşmayı teşvik eder. Bu nedenle, asal sayıların derinliği, hem matematiksel düşüncenin gelişimi hem de günlük yaşamda matematiğin rolü açısından son derece değerlidir.