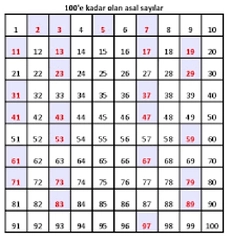
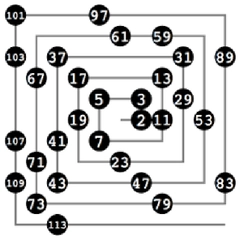
Asal sayılar, yalnızca 1 ve kendisi olmak üzere tam böleni olan doğal sayılardır. Bu özellikleri nedeniyle matematikte önemli bir yer tutarlar ve sayılar teorisinin temel yapı taşlarını oluştururlar. Bu makalede, 1'den 20'ye kadar olan asal sayıları inceleyeceğiz ve asal sayıların özellikleri ile matematiksel önemine değineceğiz.Asal Sayılar Nedir?Asal sayılar, yalnızca iki pozitif tam böleni olan doğal sayılardır. Bir asal sayının tanımı gereği, 1 ve kendisi dışındaki hiçbir sayıya tam olarak bölünemez. Asal sayılar, matematiksel hesaplamalar, kriptografi ve bilgisayar bilimleri gibi birçok alanda önemli bir rol oynamaktadır. 1'den 20'ye Kadar Asal Sayılar1'den 20'ye kadar olan asal sayılar şunlardır:
Asal Sayıların ÖzellikleriAsal sayılar, birçok matematiksel özelliğe sahiptir. Bu özellikler, asal sayı teorisinin temelini oluşturur. Aşağıda asal sayıların bazı önemli özelliklerini bulabilirsiniz:
Asal Sayıların Matematikteki ÖnemiAsal sayılar, matematiksel teorilerde ve uygulamalarda önemli bir rol oynar. İşte asal sayıların matematikteki bazı önemli alanları:
SonuçAsal sayılar, 1'den 20'ye kadar olan doğal sayılar arasında belirli bir özellik taşıyan önemli matematiksel nesnelerdir. Bu sayılar, matematiksel teoriler ve pratik uygulamalar açısından büyük bir öneme sahiptir. 1'den 20'ye kadar olan asal sayılar, sayı teorisi ve diğer matematiksel alanlarda önemli bir yer tutmaktadır. Asal sayıların incelenmesi, matematiksel düşünce ve problem çözme becerilerinin geliştirilmesine katkıda bulunur. Ekstra BilgilerAsal sayılar, sadece matematiksel bir kavram olmanın ötesinde, birçok bilim dalında da kullanılmaktadır. Örneğin, bilgisayar bilimi ve kriptografi alanında, asal sayılar şifreleme algoritmalarının temelini oluşturur. Ayrıca, asal sayıların dağılımı üzerine yapılan çalışmalar, matematiksel istatistikler ve analizler için önemli veriler sunar. Asal sayılar, doğal sayıların temel yapı taşları olarak kabul edilir ve matematiğin birçok alanında önemli bir rol oynamaktadır. Bu nedenle, asal sayıların incelenmesi ve anlaşılması, matematiksel düşüncenin geliştirilmesi açısından kritik bir öneme sahiptir. |
Asal sayılar hakkında yazdıklarınızı okudum ve gerçekten çok ilginç bir konuya değinmişsiniz. Asal sayıların sadece 1 ve kendisi dışında tam böleni olmayan doğal sayılar olduğunu belirtmeniz, bu sayıların ne kadar özel olduğunu vurguluyor. 1'den 20'ye kadar olan asal sayıları listelemeniz, bu sayıları daha iyi anlamamıza yardımcı oluyor. Ayrıca, asal sayıların kriptografi gibi önemli alanlarda kullanıldığını belirtmeniz, matematiğin pratik uygulamalarını da gözler önüne seriyor. Özellikle büyük asal sayıların şifreleme algoritmalarındaki rolü, günümüzdeki dijital güvenliğin temellerinden birini oluşturuyor. Asal sayıların sonsuz olduğunu ve ilk asal sayının 2 olduğunu bilmek, matematiksel düşüncenin derinliğini artırıyor. Bu sayılar üzerinde yapılan çalışmalar, hem teorik matematikte hem de uygulamalı alanlarda birçok kapıyı açıyor. Sizce asal sayıların daha fazla keşfedilmesi, gelecekte hangi alanlarda devrim yaratabilir?
Cevap yazBuminhan,
Asal Sayıların Önemi
Asal sayılar, matematikteki en temel yapı taşlarından biridir ve gerçekten de ilginç bir konudur. Sadece 1 ve kendisi dışında tam böleni olmayan bu sayılar, birçok matematiksel teorinin temelini oluşturur.
Asal Sayıların Uygulamaları
Kriptografi alanındaki önemi, günümüz dijital dünyasında güvenliğin sağlanmasında kritik bir rol oynamaktadır. Büyük asal sayılar, şifreleme algoritmalarının temelinde yer alarak verilerin korunmasını sağlar. Bu durum, dijital iletişimin ve finansal işlemlerin güvenliğini artırır.
Sonsuzluğun Keşfi
Asal sayıların sonsuz olduğu gerçeği, matematiksel düşüncenin derinliğini artırarak yeni keşifler için bir zemin oluşturur. Bu sayılar üzerinde yapılacak çalışmalar, hem teorik matematikte hem de uygulamalı alanlarda yeni perspektifler kazandırabilir.
Gelecekteki Olası Devrimler
Asal sayıların daha fazla keşfedilmesi, özellikle yapay zeka, veri analizi ve siber güvenlik gibi alanlarda devrim niteliğinde değişikliklere yol açabilir. Örneğin, daha etkili şifreleme yöntemleri ve veri koruma teknikleri geliştirmek için asal sayılara dayalı yeni algoritmalar araştırılabilir. Ayrıca, asal sayıların özellikleri üzerinde daha fazla çalışma yapılması, matematiksel teorilerin genişlemesine ve yeni uygulamaların ortaya çıkmasına olanak tanıyabilir.
Sonuç olarak, asal sayılar sadece matematiksel bir konu olmanın ötesinde, modern teknolojinin ve güvenliğin temel taşlarını oluşturuyor.