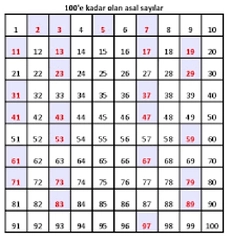
Asal sayılar, sadece 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Matematiğin temel konularından biri olan asal sayılar, sayı teorisi içerisinde önemli bir yere sahiptir. Bu makalede, 1'den 10'a kadar olan asal sayılar incelenecek ve bu sayılar hakkında detaylı bilgiler sunulacaktır. Asal Sayıların TanımıAsal sayı, 1 ve kendisi dışında hiçbir pozitif böleni olmayan doğal sayıdır. Örneğin, 2 bir asal sayıdır çünkü onun sadece iki böleni vardır: 1 ve 2. Ancak 4, 1, 2 ve 4 bölenlerine sahip olduğu için asal bir sayı değildir. 1'den 10'a Kadar Olan Asal Sayılar1'den 10'a kadar olan asal sayılar şunlardır:
Asal Sayıların ÖzellikleriAsal sayılar, çeşitli matematiksel ve pratik uygulamalarda önemli bir rol oynamaktadır. Aşağıda asal sayıların bazı temel özellikleri sıralanmıştır:
Asal Sayıların Kullanım AlanlarıAsal sayılar, hem teorik matematikte hem de pratik uygulamalarda geniş bir kullanım alanına sahiptir. Bu alanlardan bazıları şunlardır:
Sonuç1'den 10'a kadar olan asal sayılar, matematiksel olarak önemli bir yer tutmaktadır. Bu sayıların özellikleri, çeşitli alanlarda uygulamaları ve teorik matematikteki rolleri, asal sayıların önemini artırmaktadır. Asal sayılar, sayı teorisinin temel yapı taşlarını oluştururken, aynı zamanda modern teknolojinin temelini oluşturan kriptografi gibi alanlarda da kritik bir rol oynamaktadır. Ekstra BilgilerAsal sayılar, matematikçiler tarafından yüzyıllardır incelenmektedir. Örneğin, 19. yüzyılda matematikçi Carl Friedrich Gauss, asal sayıların dağılımını incelemiş ve asalların sayısının belirli bir aralıkta nasıl değiştiğini ortaya koymuştur. Ayrıca, asal sayıların sonsuzluğu, matematiksel bir teorem olarak kanıtlanmıştır. Bu nedenle asal sayılar, yalnızca teorik matematikte değil, aynı zamanda günlük yaşamda da önemli bir yere sahiptir ve bu sayılar üzerine yapılan araştırmalar günümüzde de devam etmektedir. |
Asal sayılar hakkında verdiğin bilgiler gerçekten ilginç. Özellikle 1'den 10'a kadar olan asal sayıları öğrenmek, matematiksel temelleri anlamak açısından oldukça önemli. 2'nin tek çift asal sayı olması ve diğerlerinin hepsinin tek olması dikkat çekici bir özellik. Asal sayıların kriptografi ve algoritmalar üzerindeki etkisi hakkında daha fazla bilgi edinmek, bu konulara ilgi duyanlar için faydalı olabilir. Ayrıca, Carl Friedrich Gauss'ın asal sayıların dağılımını incelemesi ve bu alandaki katkıları da matematik tarihine ışık tutuyor. Sizce asal sayıların günlük yaşamda nasıl daha fazla kullanılabileceğine dair örnekler var mı?
Cevap yazKeşşaf,
Asal Sayıların Günlük Hayattaki Kullanımı
Asal sayılar, matematikte önemli bir yere sahip olmasının yanı sıra günlük yaşamda da çeşitli alanlarda kullanılıyor. Özellikle kriptografi alanında, veri güvenliğini sağlamak için asal sayılar sıklıkla tercih ediliyor. Örneğin, online bankacılık işlemleri ve şifreleme sistemleri, asal sayılara dayanan matematiksel algoritmalara dayanarak çalışır. Bu sayede kullanıcıların bilgileri güvenli bir şekilde korunur.
Örnekler ve Uygulamalar
Ayrıca, asal sayılar bilgisayar bilimlerinde de kullanılır; örneğin, hash fonksiyonları ve veri yapıları gibi konularda. Bunun yanı sıra, asal sayılar oyun teorisi ve rastgele sayı üretiminde de önemli bir rol oynar. Bazı oyunlarda stratejik kararlar almak için asal sayılardan yararlanılabilir.
Sonuç
Asal sayıların günlük hayattaki etkisi ve uygulama alanları oldukça geniş. Bu yüzden, asal sayılar hakkında daha fazla bilgi edinmek, hem matematiksel bakış açısını geliştirmek hem de modern teknolojinin nasıl çalıştığını anlamak açısından faydalı olabilir.