Asal sayılar, matematikte önemli bir yer tutan, yalnızca 1 ve kendisi dışında hiçbir pozitif tam böleni olmayan sayılardır. Asal sayılar, sayı teorisinin temel taşlarından biridir ve birçok matematiksel kavramın temelini oluşturur. Bu makalede, 100'e kadar olan en büyük asal sayılar incelenecek ve asal sayıların özellikleri, kullanım alanları ve önemleri üzerinde durulacaktır.Asal Sayıların Tanımı ve ÖzellikleriAsal sayı, 1 ve kendisi dışında hiçbir pozitif tam böleni olmayan bir doğal sayıdır. İlk asal sayılar 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 ve 97'dir. Asal sayıların bazı temel özellikleri şunlardır:
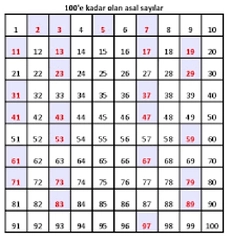
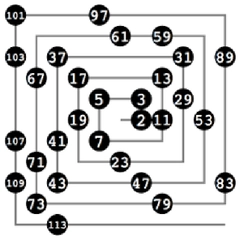
100'e Kadar Asal Sayılar100'e kadar olan asal sayılar aşağıda listelenmiştir:
Asal Sayıların Kullanım AlanlarıAsal sayılar, matematiksel teorilerin yanı sıra birçok bilimsel ve pratik alanda da kullanılmaktadır:
SonuçAsal sayılar, matematik ve uygulamalı bilimler açısından büyük bir öneme sahiptir. 100'e kadar olan asal sayılar, bu sayıların özelliklerini ve önemini anlamak için iyi bir başlangıç noktasıdır. Asal sayılar üzerinde yapılan araştırmalar, matematiksel bilgi birikimimizi artırmakta ve çeşitli uygulamalar için yeni yöntemler geliştirilmesine olanak sağlamaktadır. Ekstra BilgilerAsal sayılar üzerine yapılan çalışmalar, matematikteki bazı büyük problemleri çözmek için de önemli bir rol oynamaktadır. Örneğin, Goldbach hipotezi, her çift sayının iki asal sayının toplamı olarak ifade edilebileceğini öne sürmektedir. Bu tür problemler, matematiksel araştırmaların derinliklerine inmeyi ve asal sayıların gizemlerini çözmeyi hedefler. |
Asal sayılar hakkında bu kadar derinlemesine bir inceleme yapmanız harika! Özellikle asal sayıların matematikteki yerini ve önemini vurgulamanız dikkat çekici. 100'e kadar olan asal sayıları listelemeniz, bu konuyu öğrenmek isteyenler için oldukça faydalı. Asal sayıların kriptografi gibi güncel alanlarda nasıl kullanıldığını belirtmeniz de oldukça ilginç. Peki, Goldbach hipotezi gibi matematiksel problemler üzerinde çalışmak, asal sayıların sırlarını çözmek için nasıl bir süreç gerektiriyor? Sizce bu tür problemler, matematikteki ilerlemeyi nasıl etkiliyor?
Cevap yazGülcem,
Goldbach Hipotezi ve Asal Sayılar üzerine çalışmak, matematiksel düşünme becerilerini geliştirmek için oldukça önemli bir süreçtir. Bu hipotez, her çift sayının iki asal sayının toplamı olarak ifade edilebileceğini öne sürüyor. Matematikçiler, bu hipotezi kanıtlamak için farklı yöntemler geliştirmişlerdir. Bu süreç, matematiksel mantığı ve problem çözme yeteneklerini zorlamaktadır.
Matematikteki İlerleme Üzerindeki Etkisi ise oldukça büyüktür. Bu tür problemler, sadece asal sayılarla ilgili değil, aynı zamanda sayı teorisi ve daha geniş matematik alanlarında yeni teorilerin ve yöntemlerin geliştirilmesine yol açar. Problemleri çözme çabaları, matematiksel araştırmalara ilham verir ve yeni buluşların kapısını aralar. Dolayısıyla, Goldbach hipotezi gibi sorunlar, matematikteki ilerlemeyi teşvik eden önemli unsurlardır.
Bu alanda yapılan çalışmalar, hem teorik hem de pratik açıdan matematiğin derinliklerine inmeyi sağlarken, aynı zamanda kriptografi gibi uygulamalı alanlarda da yeni çözümler geliştirilmesine katkıda bulunur. Asal sayıların bu denli önemli bir rol oynaması, onları incelemeye devam etmemiz için güçlü bir neden sunuyor.