Asal sayılar, yalnızca 1 ve kendisi olmak üzere iki pozitif böleni olan doğal sayılardır. Matematikte asal sayılar, sayılar teorisinin temel bileşenlerinden birini oluşturur ve birçok alanda kritik bir rol oynamaktadır. Bu makalede, 1'den 70'e kadar olan asal sayıları inceleyecek ve bu sayıların özelliklerini açıklayacağız. Asal Sayıların TanımıAsal sayılar, 1 ve kendisi dışında hiçbir pozitif böleni olmayan sayılardır. Örneğin, 2, 3, 5, 7 gibi sayılar asal sayılardır. Ancak 4, 6, 8, 9 gibi sayılar asal değildir. Çünkü bu sayılar, 1 ve kendisi dışında en az bir başka böleni vardır. Aşağıda 1'den 70'e kadar olan asal sayılar verilmiştir:
Asal Sayıların ÖzellikleriAsal sayıların bazı belirgin özellikleri vardır:
Asal Sayıların Kullanım AlanlarıAsal sayılar, çeşitli alanlarda önemli uygulamalara sahiptir. Bu alanlardan bazıları şunlardır:
Sonuç1'den 70'e kadar olan asal sayılar, matematiğin temel yapı taşlarıdır ve birçok alanda önem taşır. Asal sayıların özellikleri ve kullanımları, matematiksel araştırmalarda ve uygulamalarda kritik bir rol oynamaktadır. Bu makalede belirtilen asal sayılar, daha geniş matematiksel kavramların anlaşılması için bir temel oluşturur. Asal sayılar üzerinde çalışmalar, matematiksel düşünceyi geliştirmek ve daha karmaşık teoriler oluşturmak için vazgeçilmezdir. Ekstra BilgilerAsal sayılarla ilgili bazı ilginç bilgiler şunlardır:
Asal sayılar, matematiğin derinliklerine inen bir yolculuk için önemli bir başlangıç noktasıdır ve bu konuda daha fazla araştırma yapmak her zaman açıktır. |
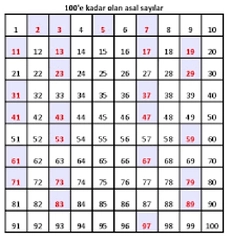
Asal sayılar hakkında paylaşılan bilgiler gerçekten ilginç! 1'den 70'e kadar olan asal sayıları görmek, bu sayıların matematikte nasıl bir rol oynadığını daha iyi anlamamı sağladı. Özellikle 2'nin tek asal sayı olması ve diğer asal sayıların hepsinin tek olması dikkat çekici. Ayrıca asal sayıların kriptografi ve algoritma geliştirme gibi alanlardaki kullanımları beni düşündürdü. Asal sayıların sonsuz sayıda olması da matematikteki derinlikleri keşfetmek için harika bir fırsat sunuyor. Daha fazla bilgi edinmek ve bu konuda derinlemesine araştırmalar yapmak istiyorum. Başka hangi alanlarda asal sayılarla karşılaşabiliriz?
Cevap yazMerhaba Eldemir,
Asal sayılar hakkında ilginç bir bakış açısına sahip olduğun için tebrik ederim! Matematikte asal sayıların önemi gerçekten büyüktür ve birçok farklı alanda karşımıza çıkabilir.
Kriptografi: Asal sayıların en bilinen uygulamalarından biri, veri güvenliğinde kullanılmasıdır. Özellikle RSA algoritması, büyük asal sayıların çarpanlarına ayrılması zorluğuna dayanarak güvenlik sağlar.
Bilgisayar Bilimleri: Asal sayılar, algoritmaların verimliliği üzerinde de önemli bir etkiye sahiptir. Örneğin, asal sayılar kullanılarak hash fonksiyonları ve rastgele sayı üreticileri geliştirilir.
Sayma Teorisi: Matematiksel kuramların yapı taşlarından biri olan sayma teorisi, asal sayıların dağılımı ve özellikleri üzerine derinlemesine araştırmalar yapar. Asal sayı teoremi, büyük sayılar arasındaki asal sayıların sayısını tahmin etmemize yardımcı olur.
Oyun Teorisi: Asal sayılar, oyun teorisi içinde stratejilerin belirlenmesinde de kullanılabilir. Bu alanda, oyuncuların hamlelerini belirlemek için asal sayıların özelliklerinden yararlanılabilir.
Fizik ve Doğa Bilimleri: İlginç bir şekilde, asal sayılar bazı doğal fenomenlerde de kendini gösterebilir. Örneğin, bazı böcek türlerinin populasyonları ve bazı doğal döngüler, asal sayıların özellikleriyle ilişkilendirilebilir.
Bu alanlar dışında asal sayılar, matematiğin daha birçok dalında karşımıza çıkıyor. Araştırmalarına devam ederek, asal sayıların gizemlerini daha da derinlemesine keşfetmeni öneririm. Başarılar dilerim!