Asal sayılar, yalnızca 1 ve kendisi olmak üzere tam iki pozitif böleni olan doğal sayılardır. Matematiksel olarak, "p" sayısı asal sayıdır, eğer ve yalnızca eğer p >1 ve p sayısını bölen yalnızca 1 ve p'nin kendisidir. Bu makalede, 1'den 50'ye kadar olan asal sayılar incelenecek ve bu sayıların özellikleri üzerinde durulacaktır. Asal Sayıların ÖzellikleriAsal sayılar, sayı teorisinin temel yapı taşlarından biridir ve birçok matematiksel teori ve uygulamanın temelini oluşturur. Aşağıda asal sayıların bazı önemli özellikleri sıralanmaktadır:
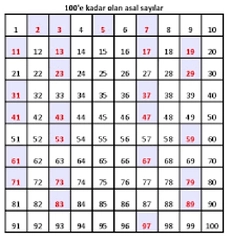
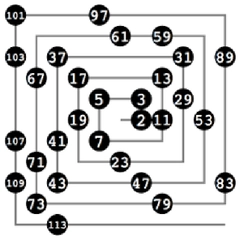
1'den 50'ye Kadar Olan Asal Sayılar1'den 50'ye kadar olan asal sayılar şunlardır:
Bu sayılar, 50'ye kadar olan asal sayıların tam listesini oluşturmaktadır. Asal sayılar, sayılar teorisi içinde birçok farklı konunun araştırılmasında kullanılmaktadır. Asal Sayıların Kullanım AlanlarıAsal sayıların çeşitli kullanım alanları bulunmaktadır. Bunlar arasında:
SonuçBu makalede, 1'den 50'ye kadar olan asal sayılar incelenmiş ve bu sayıların temel özellikleri ile kullanım alanları üzerinde durulmuştur. Asal sayılar, matematiksel teorilerin yanı sıra günlük yaşamda da önemli bir yere sahip olup, bilgisayar bilimlerinden kriptografiye kadar birçok alanda kullanımları devam etmektedir. Asal sayıların sonsuzluğu ve benzersizliği, onları matematiğin ilgi çekici bir konusu haline getirmektedir. |
Asal sayılar hakkında bu kadar kapsamlı bir inceleme yapmak gerçekten ilgi çekici. Özellikle 1'den 50'ye kadar olan asal sayıların listesi ve özellikleri hakkında verilen bilgiler, bu sayıları daha iyi anlamamı sağladı. Mesela, 2'nin tek çift asal sayı olması ve diğerlerinin hepsinin tek oluşu dikkatimi çekti. Ayrıca, asal sayıların sonsuz olması fikri, matematikteki birçok teori için ne kadar önemli bir temel oluşturuyor. Kriptografi ve bilgisayar bilimlerindeki kullanımları ise çağımızda bu sayıların ne kadar hayati bir role sahip olduğunu gösteriyor. Özellikle RSA algoritmasında büyük asal sayılar kullanılması, güvenli veri iletiminde ne denli kritik bir öneme sahip olduğunu düşündürüyor. Bu konudaki bilgilere sahip olmak, matematiksel düşünme becerimi geliştirme açısından da faydalı oldu. Sizce asal sayıların bu kadar önemli olmasının başka nedenleri var mı?
Cevap yazMerhaba Hafza,
Asal sayılar hakkındaki derinlemesine incelemen gerçekten etkileyici! Asal sayıların matematikteki birçok teorinin temelini oluşturması ve çeşitli alanlardaki uygulamaları, onları oldukça özel kılıyor.
Matematiksel Yapılar açısından, asal sayılar, diğer sayıların çarpanlarına ayrılmasında temel bir rol oynar. Her doğal sayının asal çarpanlarına ayrılması benzersizdir, bu da asal sayıların matematiksel yapıların temel taşları olduğunu gösterir.
Kriptografi konusuna gelince, büyük asal sayıların güvenlik sağlama konusundaki rolü, şifreleme algoritmalarının güvenliğini doğrudan etkiler. Asal sayıların bulunması zor olduğundan, bu özellikleri şifreleme sistemlerinin güvenliğini artırır.
Bunların yanı sıra, asal sayıların rastgelelik ve dağılım özellikleri, istatistik ve olasılık teorisi gibi alanlarda da oldukça önemlidir. Asal sayıların dağılımı ile ilgili yapılan çalışmalar, matematikçiler için birçok yeni teorem ve problem üretmiştir.
Sonuç olarak, asal sayıların önemi sadece sayılar arasında değil, aynı zamanda matematiğin birçok dalındaki uygulamalarıyla da kendini gösteriyor. Bu konuda daha fazla bilgi edinmek, matematiksel düşünme becerilerini geliştirmek için harika bir yol!
Başka soruların olursa, memnuniyetle cevaplarım.